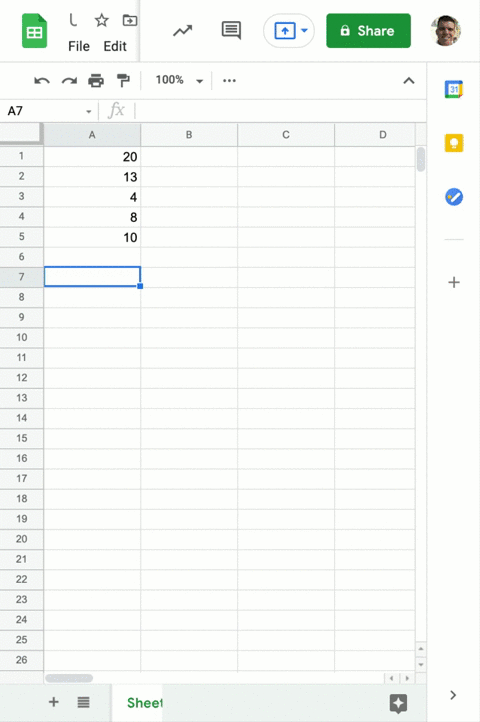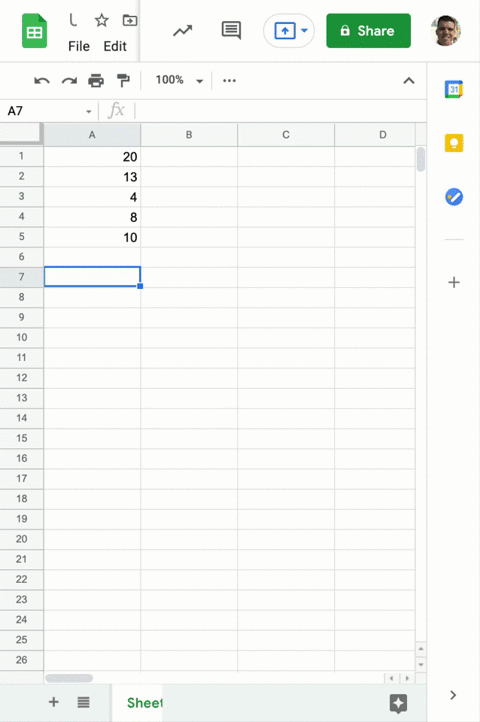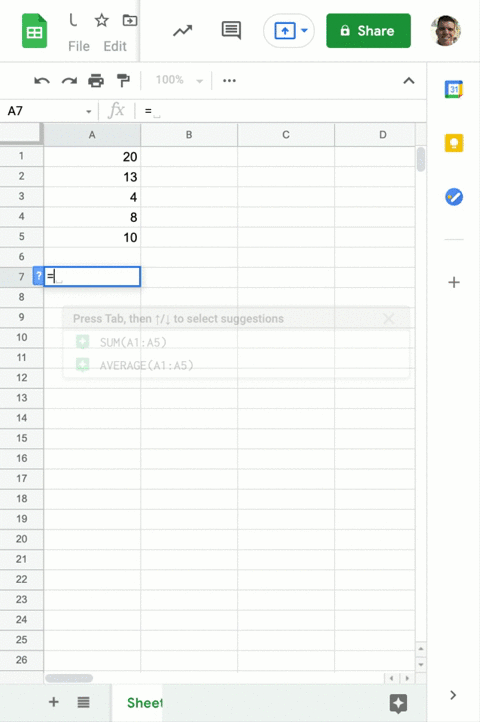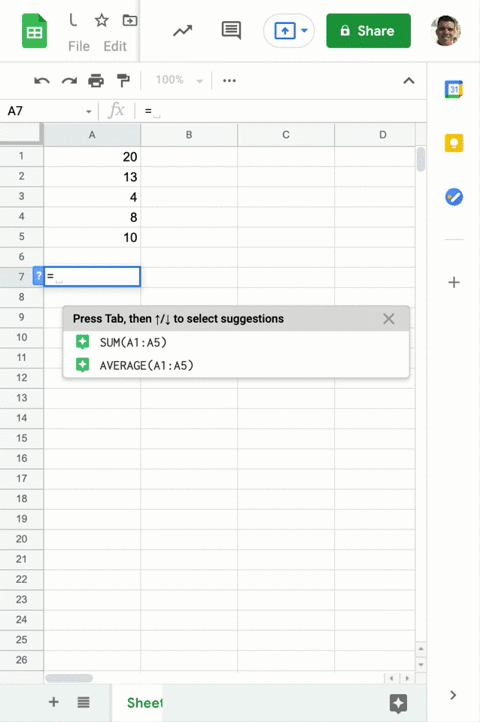
Solved Find The Population Variance And Standard Deviation Or The Population standard deviation; sample standard deviation; formula for population standard deviation. the mathematical formula to find the standard deviation of the given data is, s = [tex] \sqrt{\frac{\sum {i=1}^n (x i – x̄)^2}{n}}[ tex] where, σ is the standard deviation of the population, n is the number of observation in the population,. You can easily calculate population or sample variance and standard deviation, as well as skewness, kurtosis, and other measures, using the descriptive statistics excel calculator.
Solved By Hand Find The Population Variance And Standard Deviation Or You should calculate the sample variance when the dataset you’re working with represents a a sample taken from a larger population of interest. you should calculate the population variance when the dataset you’re working with represents an entire population, i.e. every value that you’re interested in. Find out the mean, the variance, and the standard deviation. your first step is to find the mean: so the mean (average) height is 394 mm. let's plot this on the chart: now we calculate each dog's difference from the mean: to calculate the variance, take each difference, square it, and then average the result: so the variance is 21,704. What are population and sample standard deviations. learn how to find them with their differences, including symbols, equations, and examples. You will need this to find the standard deviation for your sample. remember, variance is how spread out your data is from the mean or mathematical average. standard deviation is a similar figure, which represents how spread out your data is in your sample. in our example sample of test scores, the variance was 4.8.
Solved By Hand Find The Population Variance And Standard Deviation Or What are population and sample standard deviations. learn how to find them with their differences, including symbols, equations, and examples. You will need this to find the standard deviation for your sample. remember, variance is how spread out your data is from the mean or mathematical average. standard deviation is a similar figure, which represents how spread out your data is in your sample. in our example sample of test scores, the variance was 4.8. Like standard deviation, we can also find variance for two different types of datasets based on the sample size. they are called population variance and sample variance. we use population variance when we take all of the data in the dataset under consideration, whereas we use sample variance when we consider only a subset of the total population. Step 1: find the mean mean = (5 7 3 7 10) 5 = 32 5 = 6.4 step 2: subtract the mean from each number (and square the result) 👀 quick tip: sample vs population variance. sample variance divides by (n 1) population variance divides by n; use sample variance when working with a portion of the total data set. 📌 final formula. The distinction between population and sample standard deviation is crucial. population standard deviation (σ): used when analyzing an entire population, where every data point is known. calculated as: σ = √[Σ(xi μ)² n] where: * xi = individual data point * μ = population mean * n = total number of data points. sample standard.
Comments are closed.