Identites Remarquables Et Developpement Dexpressions Numerique

Les Identités Remarquables Education Numérique Les identités remarquables, ou égalités remarquables, sont les trois formules algébriques: ( a b ) 2 = a 2 2 ab b 2 ( a − b ) 2 = a 2 − 2 ab b 2 ( a b )( a − b ) = a 2 − b 2. Identités remarquables, application directe des formules. exercice 1 : factorisez les expressions suivantes. exercice 2 : développez les expressions suivantes.
S Entrainer Sur Les Identités Remarquables Education Numérique Les identités remarquables (3e) elles sont très utiles pour développer ou factoriser des expressions littérales rapidement. il faut les connaître dans les 2 sens. 1) carré d'une somme (a b)² = a² 2 × a × b b²; noté aussi : (a b)² = a² 2ab b². a² b² : somme des carrés. 2 × a × b ou 2ab : double produit. exemples. Développer et factoriser une expression littérale. connaître et utiliser les identités remarquables en deux directions. connaître et utiliser les règles de calcul sur les puissances. connaître et utiliser la puissance positive et négative d’un nombre relatif et rationnel. connaître et utiliser l’écriture scientifique. À levis, dans cette vidéo, nous allons voir très rapidement ce que sont les identités remarquables et comment les utiliser pour développer des expressions. les identités remarquables s'affichent sur la gauche. Présentation des trois identités remarquables: (a b)², (a b)² et a² b². démonstration : explication géométrique et algébrique. applications : développement, factorisation, simplification d’expressions.

Cours U0026 Exercices Les Identités Remarquables Se Doovi À levis, dans cette vidéo, nous allons voir très rapidement ce que sont les identités remarquables et comment les utiliser pour développer des expressions. les identités remarquables s'affichent sur la gauche. Présentation des trois identités remarquables: (a b)², (a b)² et a² b². démonstration : explication géométrique et algébrique. applications : développement, factorisation, simplification d’expressions. Pour factoriser une somme ou une différence, il y a deux possibilités : reconnaître une identité remarquable ou reconnaître un facteur commun. a) reconnaître une identité remarquable. Nous pouvons donc maintenant passer à une nouvelle notion : les identités remarquables. ces 3 formules permettent de calculer plus rapidement certaines expressions. dans ce chapitre, nous commencerons par voir le développement des identités remarquables et l'application en géométrie de ces formules. Explorez les identités remarquables avec notre cours détaillé pour les élèves de 3e année. apprenez les propriétés clés et comment les appliquer efficacement. Pour factoriser avec une identité remarquable, on utilise une des trois formules vues précédemment dans le sens inverse par rapport au développement : $ a^2 2ab b^2=(a b)^2$ $ a^2 2ab b^2=(a b)^2$.

Les Identités Remarquables Cours Dyrassa Factoriser Et Développer Pour factoriser une somme ou une différence, il y a deux possibilités : reconnaître une identité remarquable ou reconnaître un facteur commun. a) reconnaître une identité remarquable. Nous pouvons donc maintenant passer à une nouvelle notion : les identités remarquables. ces 3 formules permettent de calculer plus rapidement certaines expressions. dans ce chapitre, nous commencerons par voir le développement des identités remarquables et l'application en géométrie de ces formules. Explorez les identités remarquables avec notre cours détaillé pour les élèves de 3e année. apprenez les propriétés clés et comment les appliquer efficacement. Pour factoriser avec une identité remarquable, on utilise une des trois formules vues précédemment dans le sens inverse par rapport au développement : $ a^2 2ab b^2=(a b)^2$ $ a^2 2ab b^2=(a b)^2$.

Les Identités Remarquables Cours Dyrassa Factoriser Et Développer Explorez les identités remarquables avec notre cours détaillé pour les élèves de 3e année. apprenez les propriétés clés et comment les appliquer efficacement. Pour factoriser avec une identité remarquable, on utilise une des trois formules vues précédemment dans le sens inverse par rapport au développement : $ a^2 2ab b^2=(a b)^2$ $ a^2 2ab b^2=(a b)^2$.
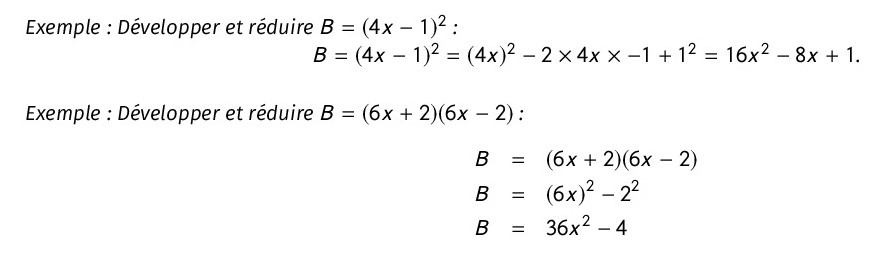
Les Identités Remarquables Cours Dyrassa Factoriser Et Développer

Comments are closed.