Posicoes Relativas Entre Reta E Plano Retas E Planos No Espaco
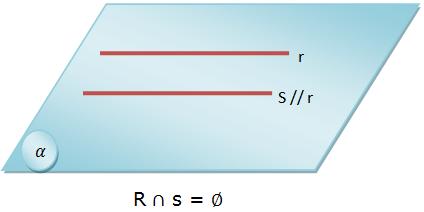
Posições Relativas Entre Duas Retas Retas E Planos No Espaço As posições relativas entre reta e plano referem se ao modo como essas figuras podem relacionar se no espaço. a reta é secante, contida ou paralela ao plano. retas são conjuntos de pontos que formam uma figura com formato de linha que não faz curva. Nesta aula de matemática você vai estudar sobre ponto, reta e plano, e suas posições relativas. ou seja, como eles podem estar organizados em formas geométricas. na aula de hoje vamos estudar os postulados da geometria e também ver posições relativas entre os entes no caso espacial.
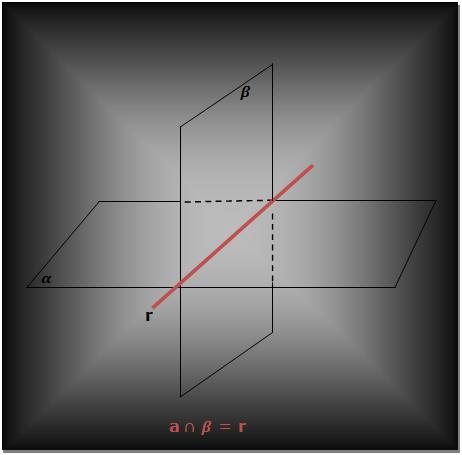
Posições Relativas Entre Dois Planos Retas E Planos No Espaço No vasto universo da geometria analítica, desvendar os segredos das retas e planos no espaço tridimensional é um desafio fascinante. neste artigo, exploraremos exercícios resolvidos que envolvem equações paramétricas, interseções de planos e direções de vetores, conduzindo você por um caminho intrigante de descobertas matemáticas. As figuras planas e espaciais são formadas pela intersecção de retas e planos pertencentes ao espaço. dentre as posições relativas, podemos destacar: retas paralelas: duas retas são paralelas se pertencerem ao mesmo plano (coplanares) e não possuírem ponto de intersecção ou ponto em comum. Começaremos com o estudo da posição relativa de duas retas no plano. lembremos primeiro que duas retas em um mesmo plano podem ser: concorrentes, ou seja, se interceptam em um único ponto. tomemos então duas retas dadas em forma vetorial como r : a vt e s : b ut. Uma reta qualquer possui três possibilidades de interação com o plano. essas possibilidades são conhecidas como posições relativas entre uma reta e um plano e estão listadas a seguir: reta contida no plano. dizemos que uma reta está contida no plano quando todos os seus pontos também são pontos do plano.

Posições Relativas Entre Reta E Plano Colégio Web Começaremos com o estudo da posição relativa de duas retas no plano. lembremos primeiro que duas retas em um mesmo plano podem ser: concorrentes, ou seja, se interceptam em um único ponto. tomemos então duas retas dadas em forma vetorial como r : a vt e s : b ut. Uma reta qualquer possui três possibilidades de interação com o plano. essas possibilidades são conhecidas como posições relativas entre uma reta e um plano e estão listadas a seguir: reta contida no plano. dizemos que uma reta está contida no plano quando todos os seus pontos também são pontos do plano. A respeito das posições relativas entre retas e planos, assinale a alternativa correta: a) duas retas distintas, r e s, são paralelas. se a reta r está contida no plano a, e a reta s está contida no plano b, então a e b jamais podem encontrar se. b) duas retas r e s são reversas. Entender as posições relativas de retas e planos é essencial para resolver questões de geometria que aparecem no enem. esses conceitos são aplicados em problemas que envolvem figuras espaciais, interseção de planos, projeções e até situações do dia a dia como construções e disposições de objetos no espaço. Um objeto de estudo da geometria analítica é a posição relativa entre duas retas no espaço, entre uma reta e um plano ou entre dois planos. neste recurso, você verá todas as possibilidades de posições relativas desses casos através de ilustrações, aprenderá um método para identificar cada caso utilizando conhecimentos da geometria. Como calcular a posição relativa de uma linha e de um plano? existem principalmente dois métodos para encontrar a posição relativa entre uma linha e um plano no espaço: por intervalos ou por vetores. quando a reta é expressa como uma equação implícita (ou geral), é mais fácil usar o método de classificação.
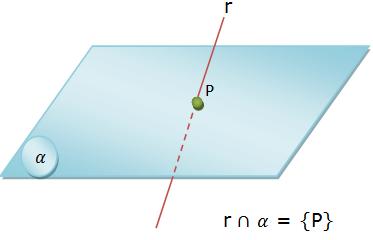
Posições Relativas Entre Reta E Plano Retas E Planos No Espaço A respeito das posições relativas entre retas e planos, assinale a alternativa correta: a) duas retas distintas, r e s, são paralelas. se a reta r está contida no plano a, e a reta s está contida no plano b, então a e b jamais podem encontrar se. b) duas retas r e s são reversas. Entender as posições relativas de retas e planos é essencial para resolver questões de geometria que aparecem no enem. esses conceitos são aplicados em problemas que envolvem figuras espaciais, interseção de planos, projeções e até situações do dia a dia como construções e disposições de objetos no espaço. Um objeto de estudo da geometria analítica é a posição relativa entre duas retas no espaço, entre uma reta e um plano ou entre dois planos. neste recurso, você verá todas as possibilidades de posições relativas desses casos através de ilustrações, aprenderá um método para identificar cada caso utilizando conhecimentos da geometria. Como calcular a posição relativa de uma linha e de um plano? existem principalmente dois métodos para encontrar a posição relativa entre uma linha e um plano no espaço: por intervalos ou por vetores. quando a reta é expressa como uma equação implícita (ou geral), é mais fácil usar o método de classificação.

Posição Relativa Entre Reta E Plano Um objeto de estudo da geometria analítica é a posição relativa entre duas retas no espaço, entre uma reta e um plano ou entre dois planos. neste recurso, você verá todas as possibilidades de posições relativas desses casos através de ilustrações, aprenderá um método para identificar cada caso utilizando conhecimentos da geometria. Como calcular a posição relativa de uma linha e de um plano? existem principalmente dois métodos para encontrar a posição relativa entre uma linha e um plano no espaço: por intervalos ou por vetores. quando a reta é expressa como uma equação implícita (ou geral), é mais fácil usar o método de classificação.

Comments are closed.