Random Variables And Discrete Distributions Tutorial 3 University Of

Lesson 2 04 Probability Distributions Of Discrete Random Variables 1.1 discrete probability distributions 3 definition 1. a random variable x is said to follow bernoulli distribu tion with parameter p if its probability mass function (p.m.f.) is given by, f x(x) = (p xq1−; x = 0,1 0 ; otherwise, where 0 < p < 1 and p q = 1. in example 1.1.2, if the die is fair and we are interested in the oc. We will open the door to the application of algebra to probability theory by introduction the concept of “random variable”. what you will need to get from it (at a minimum) is the ability to do the following “good citizen problems”. i will give you a probability mass function p(x). you will be asked to compute.

Lecture 8 Math 403 Discrete Probability Distributions Pdf S2 crv typical exam questions for continuous random variables. on studocu you find all the lecture notes, summaries and study guides you need to pass your exams with better grades. Random variables which can only take on at most a countable number of possible values are considered to be discrete random variables. each one of these possible values will be assigned some non negative probability, therefore we can intuitively as placing `mass' of probability at each possible value. Any random variable whose only possible values are 0 and 1 is called a bernoulli random variable. this is a discrete random variable – values? this distribution is specified with a single parameter: π = p(x=1) examples?. A discrete random variable is a random variable whose possible values either constitute a nite set or else can be listed in an in nite sequence. a random variable is continuous if its set of possible values consists of an entire interval on the.

3 Discrete Random Variables And Probability Distributions 3 Discrete Any random variable whose only possible values are 0 and 1 is called a bernoulli random variable. this is a discrete random variable – values? this distribution is specified with a single parameter: π = p(x=1) examples?. A discrete random variable is a random variable whose possible values either constitute a nite set or else can be listed in an in nite sequence. a random variable is continuous if its set of possible values consists of an entire interval on the. A table, formula, or graph that lists all possible values a discrete random variable can assume, together with associated probabilities, is called a discrete probability distribution. to calculate 𝑷( = ), the probability that the random variable assumes the value , add the probabilities of all the outcomes for which. University of the witwatersrand mathematical statistics 1 (stat1003) discrete random variables & some special distributions tutorial 3. suppose a particular system in a space vehicle must work properly in order for the vehicle to gain reentry into the earth’s atmosphere. one component of the system operates successfully only 80% of the time. Jason gibson discusses random variables and discrete probability distributions. he defines both terms, gives two examples showing how to use them, and shows. This course covers right from the essential concepts in probability and cover in depth on random variables (discrete and continuous) and their corresponding important distributions namely normal, binomial and geometric distributions.
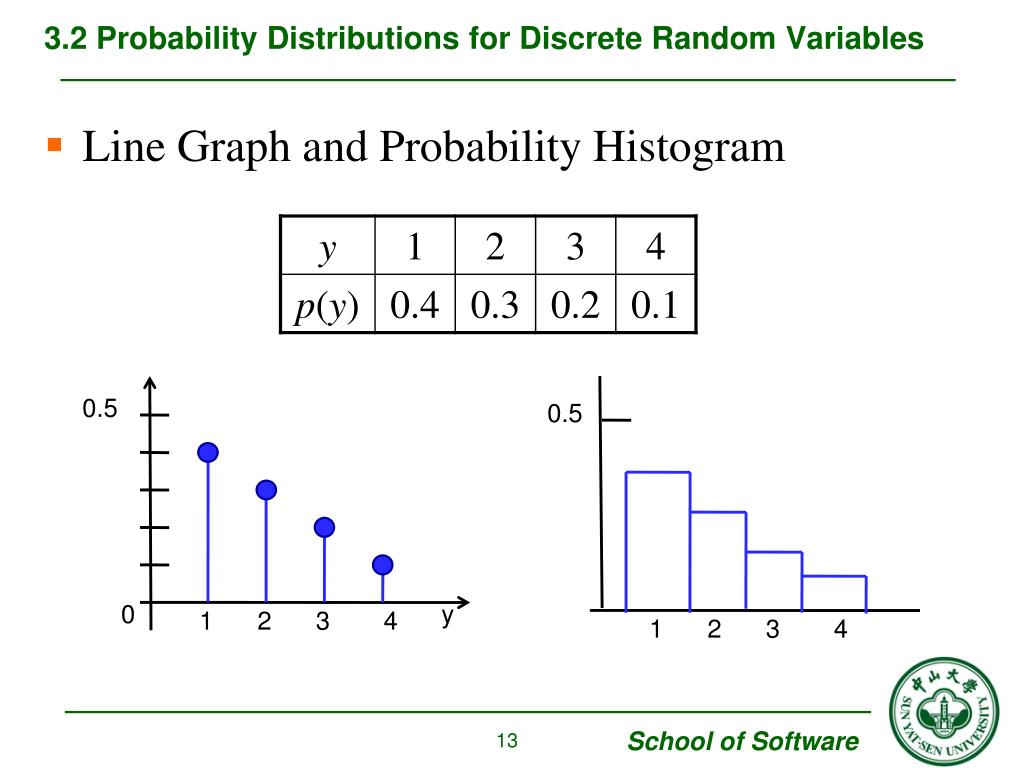
Ppt Chapter 3 Discrete Random Variables And Probability A table, formula, or graph that lists all possible values a discrete random variable can assume, together with associated probabilities, is called a discrete probability distribution. to calculate 𝑷( = ), the probability that the random variable assumes the value , add the probabilities of all the outcomes for which. University of the witwatersrand mathematical statistics 1 (stat1003) discrete random variables & some special distributions tutorial 3. suppose a particular system in a space vehicle must work properly in order for the vehicle to gain reentry into the earth’s atmosphere. one component of the system operates successfully only 80% of the time. Jason gibson discusses random variables and discrete probability distributions. he defines both terms, gives two examples showing how to use them, and shows. This course covers right from the essential concepts in probability and cover in depth on random variables (discrete and continuous) and their corresponding important distributions namely normal, binomial and geometric distributions.

Comments are closed.