Solved 3 Given P A 0 4 P B 0 5 And P A And B 0 3 A Chegg To calculate the probability of both events a and b happening (denoted as p (a and b)), we should multiply the probability of a by the probability of b given that a has already happened (p (b|a)). however, in this case, there seems to be a confusion in notation. To find p (a∪b) given p (a)= 0.6, p (b) = 0.5, and p (a|b)= 0.3, we can follow these steps: from the problem, we know p (a|b) = 0.3 and p (b)= 0.5. we can rearrange this formula to find p (a∩b): if p (a)=0.4 p (b) = 0.8 and p (b a) = 0.6 then find p (a∪b). a and b are two events such that p (a) = 0.54, p (b) = 0.69 and p (a∩b) = 0.3. find p (a∪b).
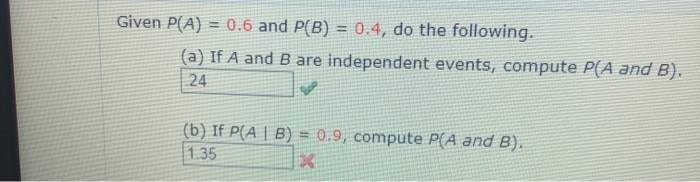
Solved Given P A 0 6 And P B 0 4 Do The Following Chegg Question: given that p (a) = 0.3, p (b) = 0.6, and p (b a) = 0.4, find p (a \cup b). P(a | b) actually means and is the same as p(a & b) p(b), where & represents the logical "and", or the intersection of the two sets. therefore, the given p(a | b) = 0.5 means that p(a & b) p(b) = 0.5. p(a & b) = 0.5*p(b) = 0.5*0.3 = 0.15. p(a or b) = p(a) p(b) p(a & b) = 0.6 0.3 0.15 = 0.75. answer. solved. The probabilities of two students a and b coming to the school in time are 3 7 and 5 7 respectively. assuming that the events, ' a coming in time' and ' b coming in time' are independent, find the probability of only one of them coming to the school in time. Question 12 (or 2nd question) if p (a) = 0.6, p (b) = 0.5 and p (a|b) = 0.3, then find p (a ∪ b).
Solved Given P A 0 3 And P B 0 6 Do The Following Chegg The probabilities of two students a and b coming to the school in time are 3 7 and 5 7 respectively. assuming that the events, ' a coming in time' and ' b coming in time' are independent, find the probability of only one of them coming to the school in time. Question 12 (or 2nd question) if p (a) = 0.6, p (b) = 0.5 and p (a|b) = 0.3, then find p (a ∪ b). The solution of 3. given that p (a) 0.3, p (b) 0.6, and p (b a) 0.4, find the followin is. To find the probability of a occurring while b does not occur (p (a and not b)), we can use the formula: p (a and not b) = p (a)×p (b′) where p (b′) is the probability of b not occurring, which can be calculated as: p (b′) = 1−p (b) =1−0.6 = 0.4. now substituting the values: p (a and not b) = 0.3×0.4 = 0.12. (iii) find p (a or b). Suppose a and b are two events such that p (n) = 0.3, p (b) = 0.4, and p (a ∪ b) = 0.75. p (a \cup b)=0.75. p(a∪b)=0.75. Latest solved 3 x 5 = 25 3 x 2 x 2 55 x 87 = 0 graph of a circle with radius 10 and center at (15, 3) 2, 9, 16, 23, 30 0.15 (y 0.2) = 2 0.5 (1 y) find the midpoint of the points (1,2) and (3, 4) find the domain and range of (7,3), ( 2, 2), (4,1), (4,1), ( 9,0) (0,7) 7, 15, 23, 31, 39, 47, 55, 63 0.003234 to scientific 1, 7, 13, 19, 25, 31, 37, 43 lcm (26,14,91) d i s tan c e (3, 8) (5, 1.
Comments are closed.