Solved In The Figure Given Below O Is The Center Of The Circle Self

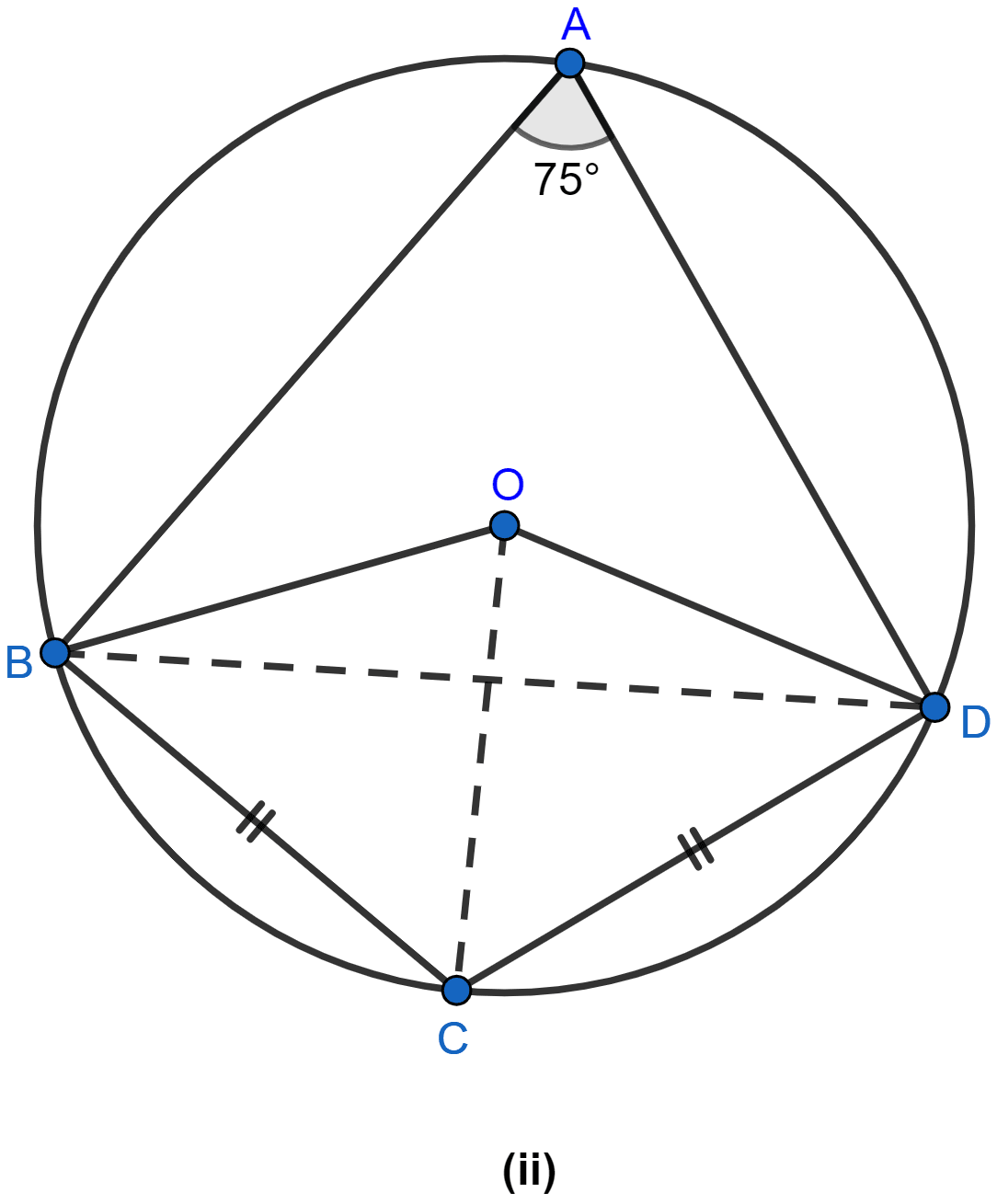
Solved In The Figure Given Below O Is The Center Of The Circle Self In the figure (ii) given below, o is the center of the circle. if ∠bad = 75° and bc = cd, find: join oc and bd as shown in the figure below: (i) ∠bod = 2 × ∠bad (∵ angle subtended by an arc at center is double the angle subtended at any point on the remaining part of the circle.) ∠bod = 2 × 75° = 150°. hence, the value of ∠bod = 150°. There are 2 steps to solve this one. we know t in the figure attached below, o is the center of the circle. which of the following must be true? attachment 1 a. ao and bo have the same length. b. ab and bo have the same length. c. ao is perpendicular to bo. d. ab is perpendicular to bo. e. abo is an equilateral triangle.
In The Figure Given Below O Is The Center Of A Circle Complete The To find $$m\angle aco$$m∠aco, subtract the given angle $$65^ {\circ}$$65∘ from $$90^ {\circ}$$90∘ because the angle at the center of the circle is $$90^ {\circ}$$90∘ minus the inscribed angle on the same arc. therefore, $$m\angle aco = 90^ {\circ} 65^ {\circ} = 25^ {\circ}$$m∠aco = 90∘ −65∘ = 25∘. Thus, the correct answer for naming a radius of the circle is option d: ao¯¯¯¯¯¯¯¯. this line segment connects the center (o) to a point (a) on the circle's circumference, fulfilling the condition of a radius. imagine a circular pizza. Given: o is the centre of circle abcp is a cyclic quadrilateral concept used : (1)we know that angle made on circumference of circle is half of the angle made on the centre of circle. (2)sum of opposite angles of quadrilateral is 180°. ∴ ∠ apc = ∠ aoc 2 calculation: ⇒ ∠ apc = 100 2 = 50° now, ⇒ ∠apc ∠abc = 180° ⇒ ∠abc. In the figure below, o is the center of the circle. name a radius of the circle. 1 identify the definition of a secant in a circle. a secant is a line that intersects a circle at two points. 2 apply the definition to the given figure.
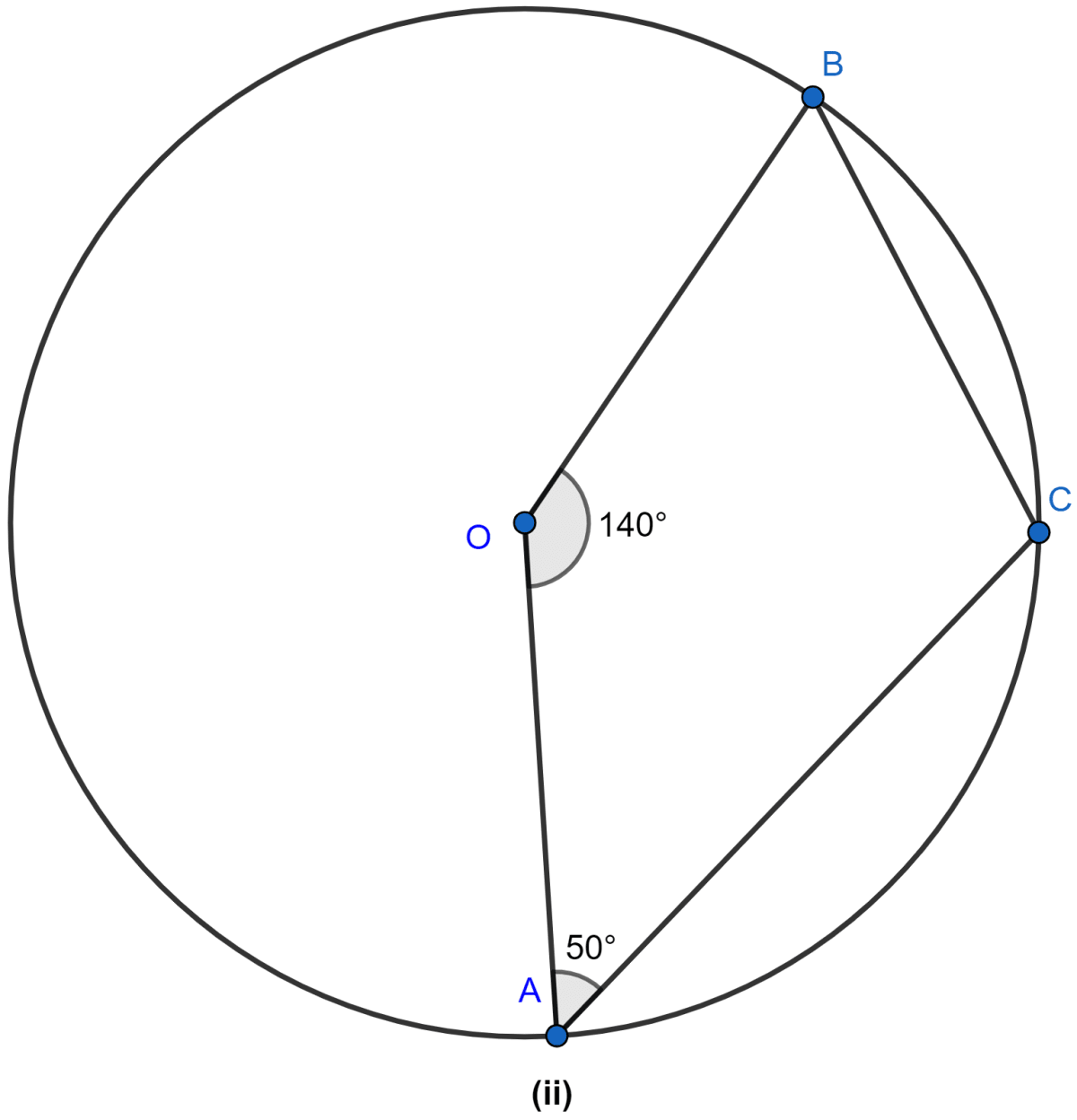
In The Figure I Given Below O Is The Center Of The Circle Given: o is the centre of circle abcp is a cyclic quadrilateral concept used : (1)we know that angle made on circumference of circle is half of the angle made on the centre of circle. (2)sum of opposite angles of quadrilateral is 180°. ∴ ∠ apc = ∠ aoc 2 calculation: ⇒ ∠ apc = 100 2 = 50° now, ⇒ ∠apc ∠abc = 180° ⇒ ∠abc. In the figure below, o is the center of the circle. name a radius of the circle. 1 identify the definition of a secant in a circle. a secant is a line that intersects a circle at two points. 2 apply the definition to the given figure. Given the figure with a circle and angles, we'll find the measure of the arcs labeled a and b. arc a. In the figure (ii) given below, o is the centre of a circle. chord cd is parallel to the diameter ab. if ∠abc = 25°, calculate ∠ced. ∴ ∠aoc = 2∠abc = 2 × 25° = 50°. hence, ∠ocd = 50°. so, ∠odc = ∠ocd. since, sum of angles of a triangle is 180°. ⇒ ∠cod = 80°. cd subtends ∠cod at center and ∠ced at point e of the circle. ⇒ ∠ced = 40°. According to the inscribed angle theorem, the angle at the circumference subtended by the same arc is half the angle at the centre subtended by the same arc. mathematically, this is represented as: x = ∠ 𝐴 𝑂 𝐵 2 . substituting the given value: x = 1 4 5 ° 2 . x = 72.5°. In the following figure, o is the centre of the circle. if op = 5 cm and radius of the circle is 3 cm, find the length of the tangent pt. if a chord of a circle of radius 11 cm is a tangent to another circle of radius 7 cm, both the circles being concentric, then the length of the chord is:.

In The Figure Ii Given Below O Is The Center Of The Knowledgeboat Given the figure with a circle and angles, we'll find the measure of the arcs labeled a and b. arc a. In the figure (ii) given below, o is the centre of a circle. chord cd is parallel to the diameter ab. if ∠abc = 25°, calculate ∠ced. ∴ ∠aoc = 2∠abc = 2 × 25° = 50°. hence, ∠ocd = 50°. so, ∠odc = ∠ocd. since, sum of angles of a triangle is 180°. ⇒ ∠cod = 80°. cd subtends ∠cod at center and ∠ced at point e of the circle. ⇒ ∠ced = 40°. According to the inscribed angle theorem, the angle at the circumference subtended by the same arc is half the angle at the centre subtended by the same arc. mathematically, this is represented as: x = ∠ 𝐴 𝑂 𝐵 2 . substituting the given value: x = 1 4 5 ° 2 . x = 72.5°. In the following figure, o is the centre of the circle. if op = 5 cm and radius of the circle is 3 cm, find the length of the tangent pt. if a chord of a circle of radius 11 cm is a tangent to another circle of radius 7 cm, both the circles being concentric, then the length of the chord is:.
In The Figure Ii Given Below O Is The Center Of The Knowledgeboat According to the inscribed angle theorem, the angle at the circumference subtended by the same arc is half the angle at the centre subtended by the same arc. mathematically, this is represented as: x = ∠ 𝐴 𝑂 𝐵 2 . substituting the given value: x = 1 4 5 ° 2 . x = 72.5°. In the following figure, o is the centre of the circle. if op = 5 cm and radius of the circle is 3 cm, find the length of the tangent pt. if a chord of a circle of radius 11 cm is a tangent to another circle of radius 7 cm, both the circles being concentric, then the length of the chord is:.

Comments are closed.