Solved Q1 3 12pts Given P A 0 35 P B 0 65 And P Ab

Solved Q1 3 12pts Given P A 0 35 P B 0 65 And P Ab Our expert help has broken down your problem into an easy to learn solution you can count on. Lessons answers archive click here to see all problems on probability and statistics question 1139643: given p (a)=0.35,p (b)=0.65 answer by ikleyn (52556) (show source):.

Solved Q1 3 12pts Given P A 0 35 P B 0 65 And P Ab To solve this, we can use the formula for the union of two events that states the probability of either event a or event b occurring is equal to the sum of the probability of each event minus the probability of a and b happening together. Given p [a]=0.35, p [b]=0.65, p [anb]=0.12, find a) p [aub], b) p [a'nb], c) p [ a b'], d) p [a’ub'], e) are a and b independent? f) p [a {b'] (conditional probability). To solve the problem, we need to find p (b) given that p (a) =0.35 and p (a∪b) =0.60, with the condition that events a and b are independent. 1. understand the relationship of probabilities: 2. use the independence condition: 3. substitute the known values: 4. rewrite the equation: 5. combine like terms: 6. isolate p (b): 7. solve for p (b): 8. Our expert help has broken down your problem into an easy to learn solution you can count on. there are 2 steps to solve this one. not the question you’re looking for? post any question and get expert help quickly.
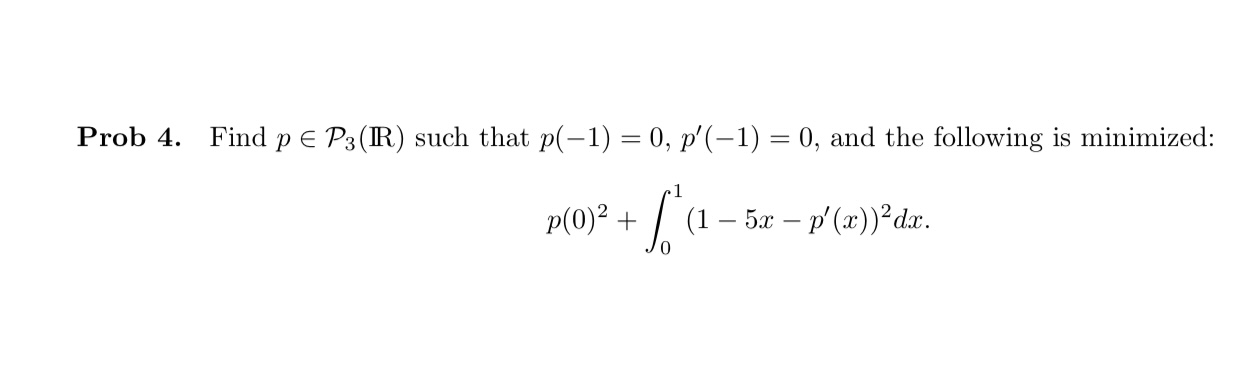
Solved Ob 4 Find P P3 R Such That P 1 0 P 1 0 And Chegg To solve the problem, we need to find p (b) given that p (a) =0.35 and p (a∪b) =0.60, with the condition that events a and b are independent. 1. understand the relationship of probabilities: 2. use the independence condition: 3. substitute the known values: 4. rewrite the equation: 5. combine like terms: 6. isolate p (b): 7. solve for p (b): 8. Our expert help has broken down your problem into an easy to learn solution you can count on. there are 2 steps to solve this one. not the question you’re looking for? post any question and get expert help quickly. To find p (a ∪ b), use the formula p (a ∪ b) = p (a) p (b) − p (a ∩ b) and substitute the given values: p (a) = 0.35, p (b) = 0.65, and p (a ∩ b) = 0.12. There are 4 steps to solve this one. the events a and b have the following probabilities. not the question you’re looking for? post any question and get expert help quickly. Using the venn diagram: we can determine the probabilities of different events by identifying the corresponding regions in the venn diagram and summing their probabilities. complement rule: the probability of an event not happening (complement) is 1 minus the probability of the event happening. Finally, we can find p (ac ∪ bc) using the formula from step 2: p (ac ∪ bc) = p (ac) p (bc) p (ac ∩ bc) = 0.65 0.35 0.12 = 0.88 so, p (ac ∪ bc) = 0.88, which is not in the given options.

Comments are closed.