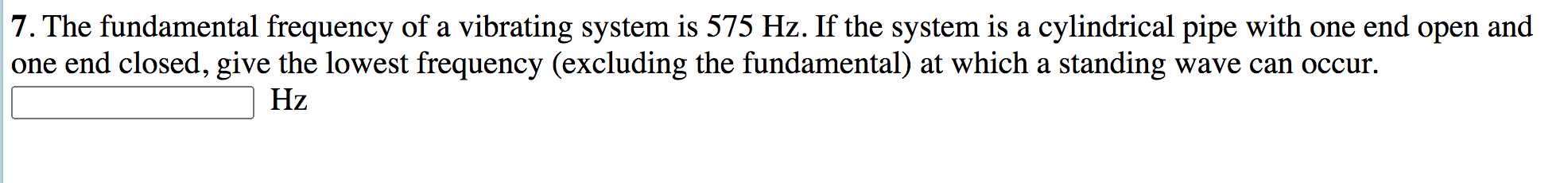
Solved 7 The Fundamental Frequency Of A Vibrating System Is Chegg Here’s the best way to solve it. the fundamental frequency of a vibrating system is 275 hz. Find step by step physics solutions and your answer to the following textbook question: the fundamental frequency of a vibrating system is 400 hz.
Solved 5 The Fundamental Frequency Of A Vibrating System Is Chegg Derive the equation of motion of a single degree of freedom system using different approaches as newton’s second law of motion and the principle of conservation of energy. For each of the following systems, give the three lowest frequencies (excluding the fundamental) at which standing waves can occur: (a) a string fixed at both ends, (b) a cylindrical pipe with both ends open, and (c) a cylindrical pipe with only one end open. The lowest frequency produced by any particular instrument is known as the fundamental frequency. the fundamental frequency is also called the first harmonic of the instrument. This page describes how it can be used in the study of vibration problems for a simple lumped parameter systems by considering a very simple system in detail. the next page describes gives a physical interpretation of the results and considers more complicated system.
Solved 5 The Fundamental Frequency Of A Vibrating System Is Chegg The lowest frequency produced by any particular instrument is known as the fundamental frequency. the fundamental frequency is also called the first harmonic of the instrument. This page describes how it can be used in the study of vibration problems for a simple lumped parameter systems by considering a very simple system in detail. the next page describes gives a physical interpretation of the results and considers more complicated system. Using stodola’s method find the fundamental mode of vibration and its natural frequency of spring mass system shown in below fig. given k1 = k2 = k3 = 1 n m, m1 = m2 = m3 = 1 kg. You can change the properties of the spring mass system (or the natural frequency and damping coefficient) and draw new amplitude v frequency curves to see how the response of the system has changed. Detailed solutions are provided for each problem, including derivation of equations of motion and determination of natural frequencies and damping ratios. initial conditions and system parameters are provided, and the response of each system is obtained. Some of these methods directly yield the natural frequency. others yield a governing equation of motion, from which the natural frequency may be determined. this tutorial focuses on rayleigh’s method, which yields the natural frequency. rayleigh's method requires an assumed displacement function.
Comments are closed.