Standard Deviation Formula Statistics Variance Sample And Population Mean

Standard Deviation Formula, Statistics, Variance, Sample And Population ...

Standard Deviation Formula, Statistics, Variance, Sample And Population ... We provide insurance, retirement and investment products and services. work with our team of remarkable people united by compassion and a genuine desire to help others. The meaning of standard is a conspicuous object (such as a banner) formerly carried at the top of a pole and used to mark a rallying point especially in battle or to serve as an emblem.

Standard Deviation Formula Using Mean And Variance At Marcia Chester Blog

Standard Deviation Formula Using Mean And Variance At Marcia Chester Blog A standard is an authoritative principle or rule that usually implies a model or pattern for guidance, by comparison with which the quantity, excellence, correctness, etc., of other things may be determined: she could serve as the standard of good breeding. Standard definition: 1. a level of quality: 2. a moral rule that should be obeyed: 3. a pattern or model that is…. learn more. Find a dentist near you and access your benefits for healthy teeth and gums. protect your vision with expert eye care and the tools and services you need to see the world clearly. protect your finances with coverage for times when a covered disability prevents you from earning a paycheck. Standard oil company was a corporate trust in the petroleum industry that existed from 1882 to 1911. the origins of the trust lay in the operations of the standard oil company (ohio), which had been founded in 1870 by john d. rockefeller. the trust was born on january 2, 1882, when a group of 41 investors signed the standard oil trust agreement, which pooled their securities of 40 companies.

PPT - Mean Variance Standard Deviation PowerPoint Presentation, Free ...

PPT - Mean Variance Standard Deviation PowerPoint Presentation, Free ... Find a dentist near you and access your benefits for healthy teeth and gums. protect your vision with expert eye care and the tools and services you need to see the world clearly. protect your finances with coverage for times when a covered disability prevents you from earning a paycheck. Standard oil company was a corporate trust in the petroleum industry that existed from 1882 to 1911. the origins of the trust lay in the operations of the standard oil company (ohio), which had been founded in 1870 by john d. rockefeller. the trust was born on january 2, 1882, when a group of 41 investors signed the standard oil trust agreement, which pooled their securities of 40 companies. A standard is a level of quality or achievement, especially a level that is thought to be acceptable. the standard of professional cricket has never been lower. The standard deduction is a specific dollar amount that reduces the amount of income on which you're taxed. your standard deduction consists of the sum of the basic standard deduction and any additional standard deduction amounts for age and/or blindness. Define standard. standard synonyms, standard pronunciation, standard translation, english dictionary definition of standard. adj. 1. serving as or conforming to an established or accepted measurement or value: a standard unit of volume. Standard meaning: 1 : a level of quality, achievement, etc., that is considered acceptable or desirable; 2 : ideas about morally correct and acceptable behavior.

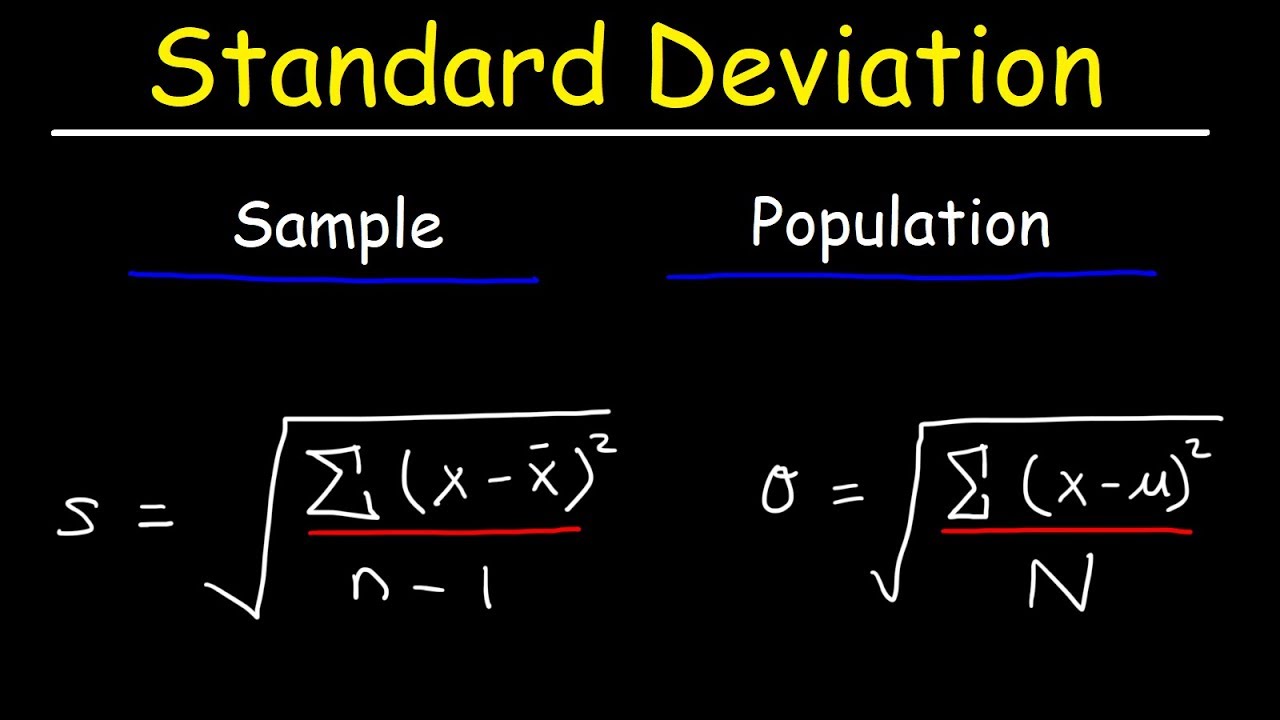
Standard Deviation Formula, Statistics, Variance, Sample and Population Mean