Sum Of Squares I Visual Proof

Sum Of Fibonacci Squares Visual Proof : R/manim

Sum Of Fibonacci Squares Visual Proof : R/manim This is a short, animated visual proof of the formula that computes that sum of the first n squares using 3 copies of the sum of squares to build a rectangle. Recently i read a "proof without words" explanation of this important formula, published by man keung siu from the university of hong kong. finally i decided to create this visualization in geogebra's 3d engine programmed by mathieu blossier and the geogebra team.

Solved The Image Below Is A Visual Proof Of Which Formula:* | Chegg.com

Solved The Image Below Is A Visual Proof Of Which Formula:* | Chegg.com This video is a compilation of five different visual proofs showing the sum formula for the sum of the first n positive squares that can be found on my channel. The closed form expression for the sum of sequence of squares was proved by archimedes during the course of his proofs of the volumes of various solids of revolution in his on conoids and spheroids. In elementary school in the late 1700s, gauss was asked to find the sum of the numbers from 1 to 100. the teacher assigned the question as basic project work, but gauss found the answer quickly by discovering a pattern. To gain full voting privileges, what is the explanation for this visual proof of the sum of squares? supposedly the following proves the sum of the first $n$ squares formula given the sum of the first $n$ numbers formula, but i don't understand it. note that it's assuming the analogous result for $1 2 \cdots n$.

A Sum Of Squares Double Sum Formula (visual Proof; 4K) : R/CasualMath

A Sum Of Squares Double Sum Formula (visual Proof; 4K) : R/CasualMath In elementary school in the late 1700s, gauss was asked to find the sum of the numbers from 1 to 100. the teacher assigned the question as basic project work, but gauss found the answer quickly by discovering a pattern. To gain full voting privileges, what is the explanation for this visual proof of the sum of squares? supposedly the following proves the sum of the first $n$ squares formula given the sum of the first $n$ numbers formula, but i don't understand it. note that it's assuming the analogous result for $1 2 \cdots n$. I offer a range of worksheets by topic , notes, past papers, practice papers and textbooks downloadable to any device from wherever you are!. Proof without words of the sum of squares formula for n =3 by cmg lee. Abstract we provide a visual proof for the inductive step of the sum of squares formula proof. In this article, we will discuss the formula to calculate the sum of squares of n natural numbers and prove it using the principle of mathematical induction. we will also discuss the formula to find the sum of squares of even and odd natural numbers and the sum of squares in geometry.

Visual Proof For Sum Of Squares With Formula Derivation : R/CasualMath

Visual Proof For Sum Of Squares With Formula Derivation : R/CasualMath I offer a range of worksheets by topic , notes, past papers, practice papers and textbooks downloadable to any device from wherever you are!. Proof without words of the sum of squares formula for n =3 by cmg lee. Abstract we provide a visual proof for the inductive step of the sum of squares formula proof. In this article, we will discuss the formula to calculate the sum of squares of n natural numbers and prove it using the principle of mathematical induction. we will also discuss the formula to find the sum of squares of even and odd natural numbers and the sum of squares in geometry.

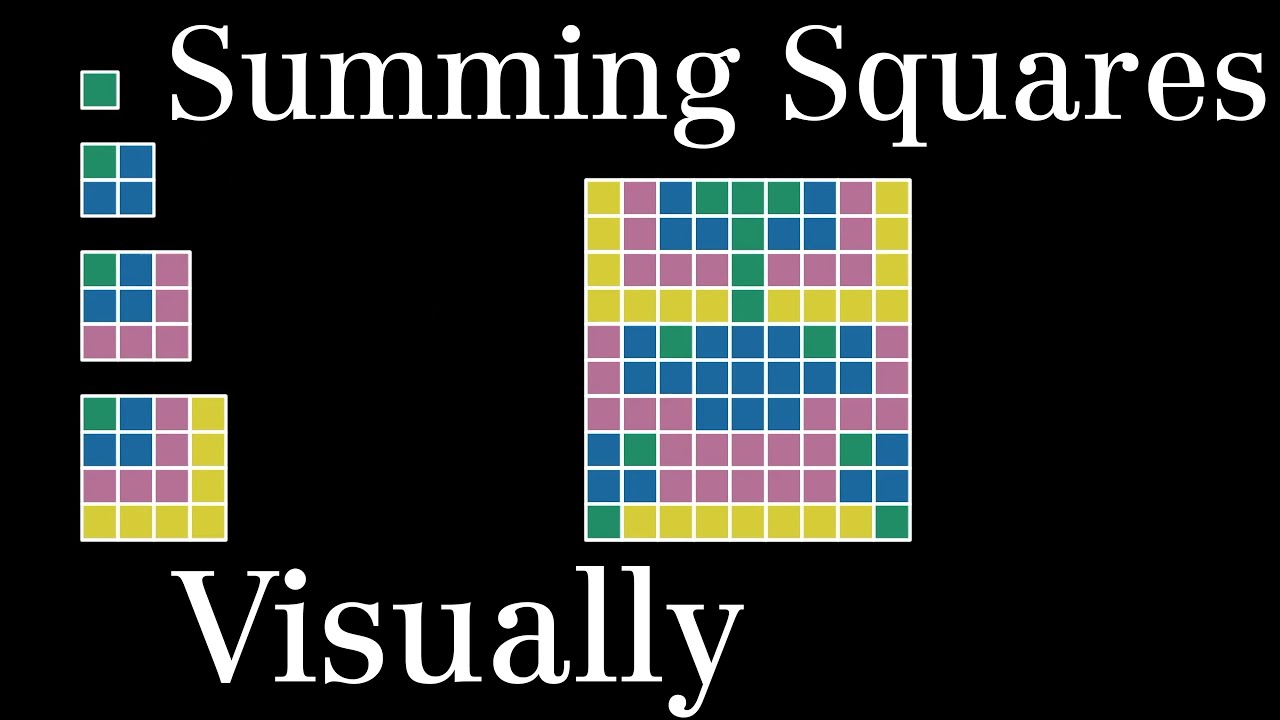
Sum of Squares I (visual proof)