The Distributive Property Math Algebra Distributiveproperty Silentmath

Distributive Property Math Mistakes The distributive property of multiplication over addition allows us to eliminate the grouping symbol, usually in the form of a parenthesis. the following diagram illustrates the basic pattern or formula how to apply it. The distributive property states that an expression of the form a(b c) can be solved as a × (b c) = ab ac. learn distributive property, types, examples & more!.

Distributive Property Math Mistakes The distributive property states that when the sum of two or more addends is multiplied by a number, it gives the same result as multiplying each addend individually by the same number and then adding the products together. Explore the comprehensive guide to all properties of math, including commutative, associative, and distributive properties. understand their applications in algebra, geometry, and calculus, and how they form the foundation of mathematical reasoning. master these essential concepts to enhance problem solving skills and deepen your mathematical knowledge. perfect for students and educators alike. The distributive property is widely used in algebra and is one of the most important properties. in this lesson, i will walk you step by step through how to properly use this property. The distributive property is a critical property of algebra. it helps us simplify expressions by combining like terms. of all the properties of numbers, it's probably the one we use the most often.

Distributive Property Worksheet The distributive property is widely used in algebra and is one of the most important properties. in this lesson, i will walk you step by step through how to properly use this property. The distributive property is a critical property of algebra. it helps us simplify expressions by combining like terms. of all the properties of numbers, it's probably the one we use the most often. Introduce students to multiple ways of using the distributive property! these attractive guided notes show multiple ways of using the distributive property, including the box method, and include practice problems (you do's) for the students. both simple numeric and algebraic examples are included. both cars. distribution? draw it!. The distributive property, also referred to as the distributive law, is a property of real numbers that states that multiplication distributes over addition. this means that multiplying by a group of numbers being added together is the same as multiplying each of the numbers in the group separately, then adding the products together. This is an example of the distributive property which can be used to find the product of a number and a sum or a difference. $$a\left ( b c \right )=\left ( b c \right )a=ab ac$$ $$a\left ( b c \right )=ab ac=ba ca=\left ( b c \right )a$$ the parts of the expression are called terms. a term could either be a number, a variable, or a product. The distributive property of algebra is about grouping terms. it states that for any real numbers \(a, b, \text{ and } c\), that : \(ac bc = (a b)c\) or.
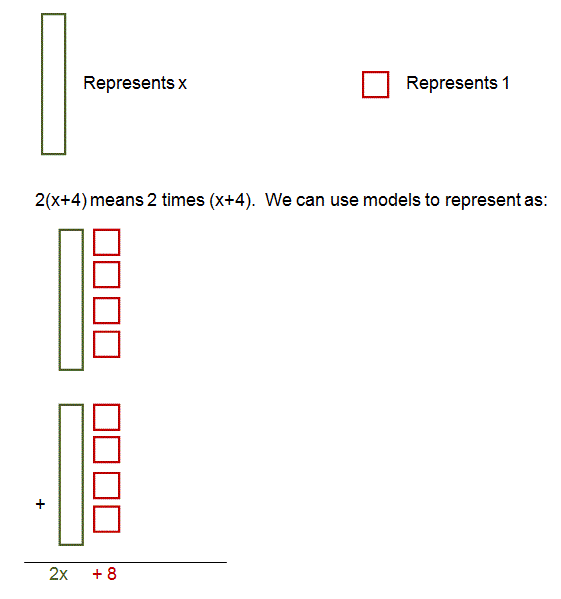
Distributive Property Introduce students to multiple ways of using the distributive property! these attractive guided notes show multiple ways of using the distributive property, including the box method, and include practice problems (you do's) for the students. both simple numeric and algebraic examples are included. both cars. distribution? draw it!. The distributive property, also referred to as the distributive law, is a property of real numbers that states that multiplication distributes over addition. this means that multiplying by a group of numbers being added together is the same as multiplying each of the numbers in the group separately, then adding the products together. This is an example of the distributive property which can be used to find the product of a number and a sum or a difference. $$a\left ( b c \right )=\left ( b c \right )a=ab ac$$ $$a\left ( b c \right )=ab ac=ba ca=\left ( b c \right )a$$ the parts of the expression are called terms. a term could either be a number, a variable, or a product. The distributive property of algebra is about grouping terms. it states that for any real numbers \(a, b, \text{ and } c\), that : \(ac bc = (a b)c\) or.

Index Of Pages Pdf Math Algebra Distributiveproperty This is an example of the distributive property which can be used to find the product of a number and a sum or a difference. $$a\left ( b c \right )=\left ( b c \right )a=ab ac$$ $$a\left ( b c \right )=ab ac=ba ca=\left ( b c \right )a$$ the parts of the expression are called terms. a term could either be a number, a variable, or a product. The distributive property of algebra is about grouping terms. it states that for any real numbers \(a, b, \text{ and } c\), that : \(ac bc = (a b)c\) or.

Comments are closed.