The Point Where All The Three Interior Angle Bisectors Of A Triangle

The Point Where All The Three Interior Angle Bisectors Of A Triangle An angle bisector of a triangle is a line segment that bisects a vertex angle of a triangle and meets the opposite side of the triangle when extended. they are also called the internal bisector of an angle. The incenter of a triangle is the intersection point of all the three interior angle bisectors of the triangle. in other words, it can be defined as the point where the internal angle bisectors of the triangle cross.

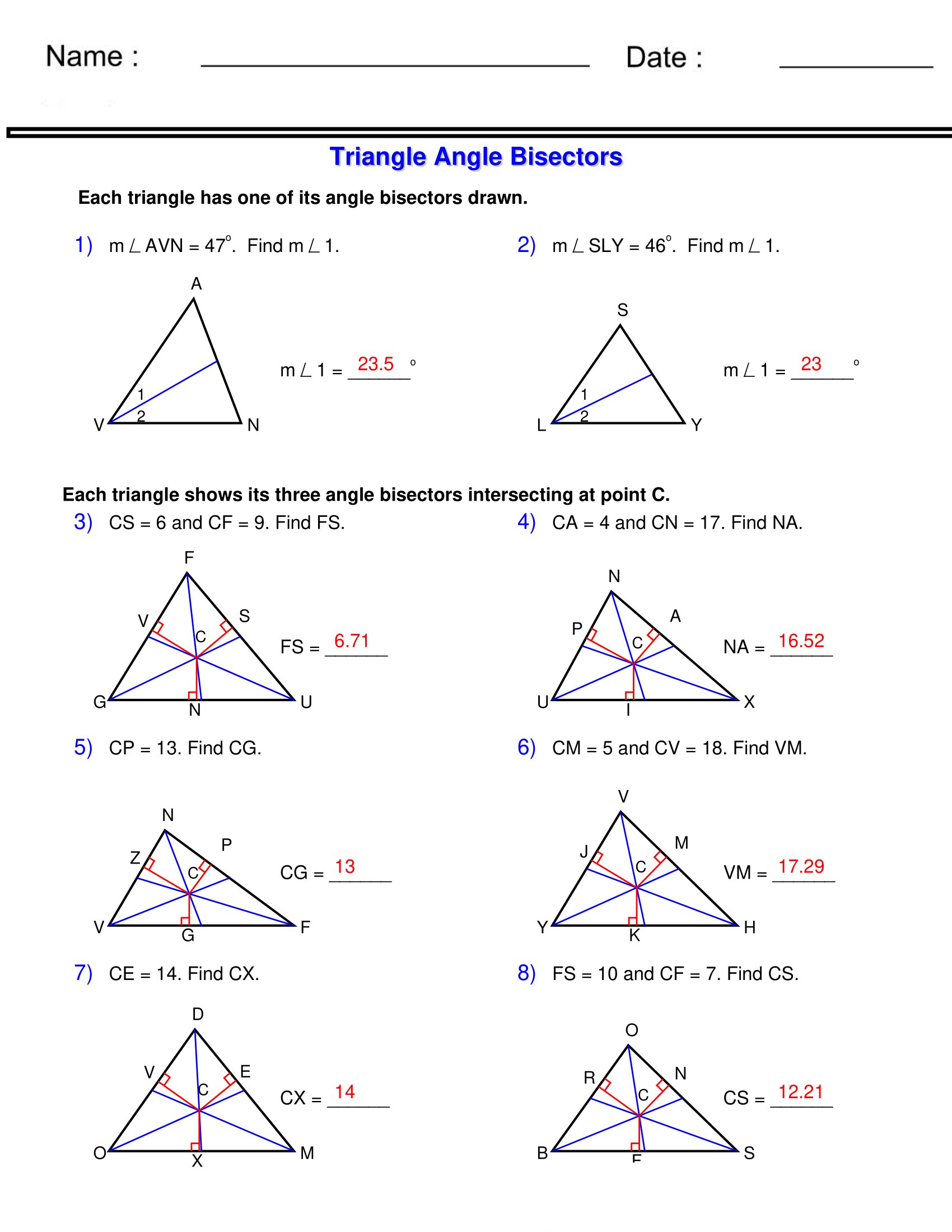
Angle Bisectors Triangle Worksheets Made By Teachers The incenter is the point of concurrency of the angle bisectors of all the interior angles of the triangle. in other words, the point where three angle bisectors of the angles of the triangle meet are known as the incenter. the incenter always lies within the triangle. The point where the three angle bisectors of a triangle intersect is called the incenter. step by step explanation: consider a triangle abc. each angle bisector splits its respective angle into two equal parts. let the angle bisectors of angles a, b, and c intersect at a point o. this point o is known as the incenter of the triangle. As the sum of all interior angles of a triangle is 180 degrees, then the sum of two interior angles cannot be equal to 360° in measure, and therefore the angle bisectors cannot be parallel. therefore, they intersect. let the letter o denote the point of intersection of two angle bisectors. Point of intersection of all three interior angle bisectors of the triangle, equidistant from sides.

In Triangle Lmn Bisectors Of Interior Angles At L And N Intersect Each As the sum of all interior angles of a triangle is 180 degrees, then the sum of two interior angles cannot be equal to 360° in measure, and therefore the angle bisectors cannot be parallel. therefore, they intersect. let the letter o denote the point of intersection of two angle bisectors. Point of intersection of all three interior angle bisectors of the triangle, equidistant from sides. The angle bisector of an angle of a triangle is a straight line that divides the angle into two congruent angles. the three angle bisectors of the angles of a triangle meet in a single point, called the incenter . The incenter of a triangle is defined as the point of intersection of all three interior angle bisectors of the triangle. in simple words, an incenter is a point where the internal bisectors of a triangle cross. this point is equidistant from the sides of a triangle, and it lies inside the triangle. The point where the three angle bisectors of a triangle intersect is known as the incenter. the incenter has the unique property of being equidistant from all three sides of the triangle. therefore, the correct answer is b. incenter. Here we will prove that the three angle bisectors of the internal angles of a triangle are concurrent. consider the arbitrary triangle abc, in which the dotted lines are bisectors of the angles b and c and p is the intersection of these angle bisectors.

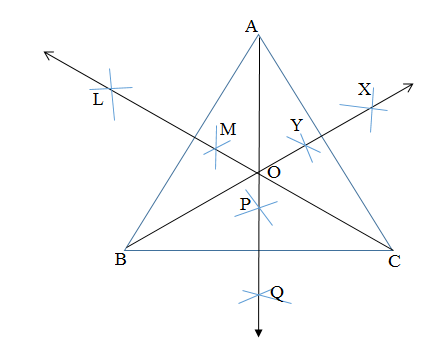
Draw A Triangle And The Perpendicular Bisectors Of All Three Sides Do The angle bisector of an angle of a triangle is a straight line that divides the angle into two congruent angles. the three angle bisectors of the angles of a triangle meet in a single point, called the incenter . The incenter of a triangle is defined as the point of intersection of all three interior angle bisectors of the triangle. in simple words, an incenter is a point where the internal bisectors of a triangle cross. this point is equidistant from the sides of a triangle, and it lies inside the triangle. The point where the three angle bisectors of a triangle intersect is known as the incenter. the incenter has the unique property of being equidistant from all three sides of the triangle. therefore, the correct answer is b. incenter. Here we will prove that the three angle bisectors of the internal angles of a triangle are concurrent. consider the arbitrary triangle abc, in which the dotted lines are bisectors of the angles b and c and p is the intersection of these angle bisectors.