Chapitre 20 La Double Distributivité Exercice 1 : lorsque c’est possible, utiliser la distributivité pour développer les expressions suivantes. si c’est impossible, expliquer pourquoi. exercice 3 : parmi ces quatre formules, quelles sont celles qui sont toujours égales ? exercice 4 : développer les expressions suivantes. Cours et exercices sur la propriété de distributivité de la multiplication sur l'addition, les développements, les factorisations et la double distributivité.
Distributivite Factoriser Développer Pdf Logique Concepts Méthode pour développer une expression. définition : développer une expression, c'est la transformer en somme. 1°) développement d'un nombre par une somme : si on considère 4 nombres relatifs, ( a , b , c , d ) (a,\;b,\;c,\;d) ( a , b , c , d ) , \;. Le cours et les exercices corrigés sur la double distributivité en 5ème . 1. la simple distributivité : pour tous nombres a, b et k on a : 2. la double distributivité : développer les expressions suivantes : simplifier les développements suivants :. Calcule mentalement en appliquant la double distributivité et complète chacune des trois cases. tu peux aussi utiliser un brouillon pour les calculs intermédiaires. cours et exemples : double distributivité. Le calcul littéral et la double distributivité dans un cours de maths en 4ème faisant intervenir la définition d’une expression littérale ou algébrique, savoir développer ou factoriser une expressions. puis nous terminerons cette leçon en quatrième avec les propriétés de la simple et double distributivité.
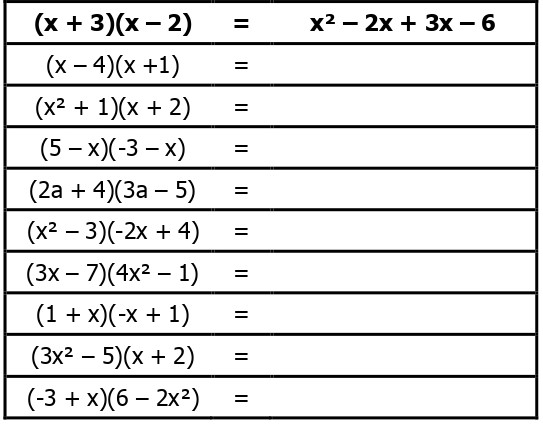
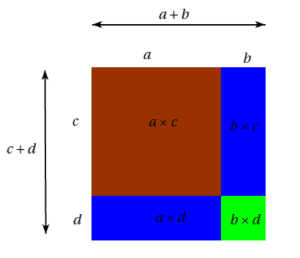
Double Distributivité Cours Et Exercices Corrigés Calcule mentalement en appliquant la double distributivité et complète chacune des trois cases. tu peux aussi utiliser un brouillon pour les calculs intermédiaires. cours et exemples : double distributivité. Le calcul littéral et la double distributivité dans un cours de maths en 4ème faisant intervenir la définition d’une expression littérale ou algébrique, savoir développer ou factoriser une expressions. puis nous terminerons cette leçon en quatrième avec les propriétés de la simple et double distributivité. Développer et factoriser $(a b)(c d)$ i) rappel . pour ce chapitre, il est bon de se souvenir de la distributivité simple : $k(a b) = ka kb$. exemples : $3(x 5)=3x 15$ $ 4(x 2)= 4x 8$ ii) développer . on chercher à développer $(a b)(c d)$, ce qui revient d’abord à développer $a$ avec $(c d)$ puis développer $b$ avec $(c d. Le développement, c’est comme déplier une expression mathématique. on transforme un produit (multiplication) en une somme ou une différence. pour cela, on utilise la distributivité. 📖. 🔑 règle de la distributivité : a × (b c) = a × b a × c. 👉 exemple : développons 3 × (x 4): on applique la distributivité : 3 × x. Pour développer il faut utiliser la distributivité simple ou double prenons les nombres a, b, c, d et m : exemple : développer et simplifier a = (x 3)(x 2) a = (x 3)(x 2) = x*x x*2 3*x 3*2 = x2 2x 3x 6 = x2 5x 6 pour factoriser une expression, il faut utiliser un facteur commun. prenons les nombres a, b, et p :. La distributivité, qu’elle soit simple ou double sert à réduire une expression littérale. en effet on va se servir de leur formule pour factoriser ou développer, suivant si notre expression est un produit à développer ou une somme (ou différence) à factoriser.
Comments are closed.